Rasyonel sayılar tam sayıların bir genişlemesidir ve Q ile gösterilir. Q kümesi genelde şöyle tanımlanır.
Rasyonel Sayıların en basit biçimi a ve b tamsayılarının ortak böleni olmadığı a/b ifadesidir.
Herhangi bir sayının sıfıra bölümü tanımsızdır.
Sıfırdan büyük olan Rasyonel Sayılara pozitif rasyonel sayılar, sıfırdan küçük olan rasyonel sayılar ise negatif rasyonel sayılar denir. Pozitif Rasyonel Sayılar kümesi ile negatif Rasyonel sayılara ise ile gösterilir.
Paydaları eşit olan rasyonel sayılar
Paydaları eşit olan rasyonel oranlar için payı büyük olan daha büyük, payı küçük olan daha küçüktür.
Örneğin
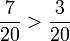
Burada paydalar eşit ve 20’dir. Pay değerleri karşılaştırılınca soldaki pay 7 sağdaki pay 3’den daha büyük olduğu için, soldaki rasyonel oran daha büyüktür.
Unutmamalıdır ki negatif paylar karşılaştırılırken sadece mutlak değerlerin karşılaştırılması hatalı olup negatif işaretlerinin de ele alınması ve :negatif sayılı pay değerlerde mutlak değeri büyük görünen sayının daha küçük olduğu hatırlanmalıdır:
Payda 20’ye eşit olup sağdaki negatif pay değeri -3, soldaki negatif pay değeri olan -7’den daha büyük olduğu için sağdaki oran daha büyüktür.
Payları eşit olan rasyonel sayılar
Payı eşit olan rasyonel sayılar için ise paydaları eşit olanın tam tersi bir kural uygulanır:
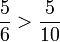
Paylar eşit olduğunda bölünen parça sayısı yani payda büyüdükçe oluşan parça boyutları daha küçük olacaktır.
Ne payları ne de paydaları eşit olan rasyonel sayılar
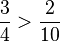
Bu şekildeki durumlarda karşılaştırmadan evvel paydaların eşitlenmesi veya içler dışlar çarpımı yapılmasını gerektirir.
Paydaların eşitlenmesi
Her iki rasyonel sayının da birbirlerinin paydalarıyla genişletilmesini gerektirir.
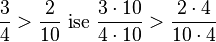
Yukarıda görüldüğü gibi genişletme işleminden sonra oluşan paydaların ikisi de 10.4 yani 40′tır. Yukarıda görüldüğü gibi karşılaştırılabilir.
İçler dışlar çarpımı ise birinci rasyonel sayının payının ikincinin paydasına, ikincinin paydasının ise birincinin payıyla çarpılmasıdır. Örnek;














